Khan Academy on a Stick
Conic sections
A detailed look at shapes that are prevalent in science: conic sections
-
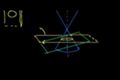 Introduction to conic sections
Introduction to conic sections
What are conic sections and why are they called "conic sections"?
Conic section basics
What is a conic other than a jazz singer from New Orleans? Well, as you'll see in this tutorial, a conic section is formed when you intersect a plane with cones. You end up with some familiar shapes (like circles and ellipses) and some that are a bit unexpected (like hyperbolas). This tutorial gets you set up with the basics and is a good foundation for going deeper into the world of conic sections.
Circles
You've seen circles your entire life. You've even studied them a bit in math class. Now we go further, taking a deep look at the equations of circles.
-
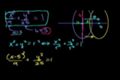 Conic sections: Intro to ellipses
Conic sections: Intro to ellipses
Introduction to the ellipse.
-
 Foci of an ellipse
Foci of an ellipse
Calculating the foci (or focuses) of an Ellipse.
Ellipses
What would you call a circle that isn't a circle? One that is is is taller or fatter rather than being perfectly round? An ellipse. (All circles are special cases of ellipses.) In this tutorial we go deep into the equations and graphs of ellipses.
-
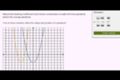 Parabola intuition example 1
Parabola intuition example 1
-
 Parabola focus and directrix 1
Parabola focus and directrix 1
Parabola as the locus of all points equidistant from a point and a line
-
 Focus and directrix of a parabola 2
Focus and directrix of a parabola 2
Finding the focus and directrix of a parabola
-
 Using the focus and directrix to find the equation of a parabola
Using the focus and directrix to find the equation of a parabola
Parabolas
You've seen parabolas already when you graphed quadratic functions. Now we will look at them from a conic perspective. In particular we will look at them as the set of all points equidistant from a point (focus) and a line (directrix). Have fun!
-
 Conic sections: Intro to hyperbolas
Conic sections: Intro to hyperbolas
Introduction to the hyperbola
-
 Conic sections: Hyperbolas 2
Conic sections: Hyperbolas 2
Continuation of the intro to hyperbolas
-
 Conic sections: Hyperbolas 3
Conic sections: Hyperbolas 3
Part 3 of the intro to hyperbolas
-
 Foci of a hyperbola
Foci of a hyperbola
Introduction to the foci (focuses) of a hyperbola
-
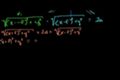 Proof: Hyperbola foci
Proof: Hyperbola foci
Proof of the hyperbola foci formula
Hyperbolas
It is no hyperbole to say that hyperbolas are awesome. In this tutorial, we look closely at this wacky conic section. We pay special attention to its graph and equation.
-
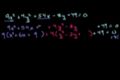 Identifying an ellipse from equation
Identifying an ellipse from equation
Part 1 of identifying and graphic conic sections
-
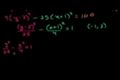 Identifying a hyperbola from an equation
Identifying a hyperbola from an equation
Part 2 of identifying and graphing conic sections
-
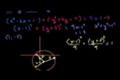 Identifying circles and parabolas from equations
Identifying circles and parabolas from equations
Let's identify (and graph) a couple of more conics!
-
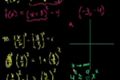 Hyperbola and parabola examples
Hyperbola and parabola examples
Parabola, Hyperbolas, etc.
Conics from equations
You're familiar with the graphs and equations of all of the conic sections. Now you want practice identifying them given only their equations. You, my friend, are about to click on exactly the right tutorial.
-
 Tangent line hyperbola relationship (very optional)
Tangent line hyperbola relationship (very optional)
How a tangent line relates to a hyperbola. Might be useful for some competitive exams where there isn't time to derive (like we are doing in this video)
-
 IIT JEE circle hyperbola common tangent part 1
IIT JEE circle hyperbola common tangent part 1
2010 IIT JEE Paper 1 Problem 45 Circle Hyperbola Common Tan
-
 IIT JEE circle hyperbola common tangent part 2
IIT JEE circle hyperbola common tangent part 2
2010 IIT JEE Paper 1 Problem 45 Circle Hyperbola Common Tangent Part 2
-
 IIT JEE circle hyperbola common tangent part 3
IIT JEE circle hyperbola common tangent part 3
2010 IIT JEE Paper 1 Problem 45 Circle Hyperbola Common Tangent Part 3
-
 IIT JEE circle hyperbola common tangent part 4
IIT JEE circle hyperbola common tangent part 4
2010 IIT JEE Paper 1 Problem 45 Circle Hyperbola Common Tangent Part 4
-
 IIT JEE circle hyperbola common tangent part 5
IIT JEE circle hyperbola common tangent part 5
2010 IIT JEE Paper 1 Problem 45 Circle Hyperbola Common Tangent Part 5
-
 IIT JEE circle hyperbola intersection
IIT JEE circle hyperbola intersection
2010 IIT JEE Paper 1 Problem 46 Circle Hyperbola Intersection
Conics in the IIT JEE
Do you think that the math exams that you have to take are hard? Well, if you have the stomach, try the problem(s) in this tutorial. They are not only conceptually difficult, but they are also hairy. Don't worry if you have trouble with this. Most of us would. The IIT JEE is an exam administered to 200,000 students every year in India to select which 2000 go to the competitive IITs. They need to make sure that most of the students can't do most of the problems so that they can really whittle the applicants down.

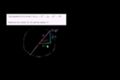 Radius and center for a circle equation in standard form
Radius and center for a circle equation in standard form Completing the square to write equation in standard form of a circle
Completing the square to write equation in standard form of a circle