Khan Academy on a Stick
Perimeter, area, and volume
A broad set of tutorials covering perimeter area and volume with and without algebra.
-
Perimeter and area: the basics
Great geometry primer on perimeter and area. Listen carefully. Sal explains the concepts so you'll understand them.
-
Triangle area proofs
Proving that the area of any triangle is 1/2 b x h
-
Interesting perimeter and area problems
Three example problems involving perimeter and area
-
Area of diagonal generated triangles of rectangle are equal
Area of Diagonal Generated Triangles of Rectangle are Equal
-
Area of an equilateral triangle
Finding the formula for the area of an equilateral triangle with side s
-
Area of shaded region made from equilateral triangles
-
Challenging perimeter problem
Perimeter of rectangle covered by 9 non-overlapping squares. From 200) American Invitational Math Exam
Perimeter and area of triangles
You first learned about perimeter and area when you were in grade school. In this tutorial, we will revisit those ideas with a more mathy lens. We will use our prior knowledge of congruence to really start to prove some neat (and useful) results (including some that will be useful in our study of similarity).
-
Triangle inequality theorem
Intuition behind the triangle inequality theorem
Triangle inequality theorem
The triangle inequality theorem is, on some level, kind of simple. But, as you'll see as you go into high level mathematics, it is often used in fancy proofs. This tutorial introduces you to what it is and gives you some practice understanding the constraints on the dimensions of a triangle.
-
Koch snowflake fractal
A shape that has an infinite perimeter but finite area
-
Area of an equilateral triangle
Finding the formula for the area of an equilateral triangle with side s
-
Area of Koch snowflake (part 1) - advanced
Starting to figure out the area of a Koch Snowflake (which has an infinite perimeter)
-
Area of Koch snowflake (part 2) - advanced
Summing an infinite geometric series to finally find the finite area of a Koch Snowflake
Koch snowflake fractal
Named after Helge von Koch, the Koch snowflake is one of the first fractals to be discovered. It is created by adding smaller and smaller equilateral bumps to an existing equilateral triangle. Quite amazingly, it produces a figure of infinite perimeter and finite area!
-
Heron's formula
Using Heron's Formula to determine the area of a triangle while only knowing the lengths of the sides
-
Part 1 of proof of Heron's formula
Part 1 of the proof of Heron's Formula
-
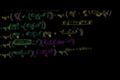Part 2 of proof of Heron's formula
Showing that the expression in part 1 is identical to Heron's Formula
Heron's formula
Named after Heron of Alexandria, Heron's formula is a power (but often overlooked) method for finding the area of ANY triangle. In this tutorial we will explain how to use it and then prove it!
-
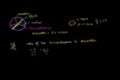Circles: radius, diameter, circumference and Pi
A circle is at the foundation of geometry and how its parts relate to each other is both completely logical and a wonder.
-
Labeling parts of a circle
Radius, diameter, center, and circumference--all are parts of a circle. Let's go through each and make sure we understand how they are defined.
-
Area of a circle
In this example, we solve for the area of a circle when given the diameter. If you recall, the diameter is the length of a line that runs across the circle and through the center.
Circumference and area of circles
Circles are everywhere. How can we measure how big they are? Well, we could think about the distance around the circle (circumference). Another option would be to think about how much space it takes up on our paper (area). Have fun!
-
Quadrilateral overview
"Quad" means "four" and "lateral" means "line." A quadrilateral is literally a shape with four sides (lines) and four angles. Let's learn the difference between concave and convex quadrilaterals as well as trapezoids, parallelograms, and rhombi.
-
Quadrilateral properties
How about this: we are given a 4-sided shape and asked to determine whether its properties qualify it to be called a quadrilateral (or category of quadrilaterals). Check it out.
-
Area of a parallelogram
Guess what's interesting about the opposite sides of a parallelogram? That's right....there are parallel! Let's find the area--base times height
-
Area of a trapezoid
A trapezoid is a cousin of the parallelogram. However, in trapezoid only two of the opposing sides are parallel to each other. Here's we explain how to find its area.
-
Area of a kite
Who doesn't like kites? If you were going to make your own out of a piece of cloth, then knowing the area of the kite would be helpful, right? Let's see how it's done.
-
Perimeter of a parallelogram
-
Perimeter and area of a non-standard polygon
Perimeter and Area of a Non-Standard Polygon
Perimeter and area of non-standard shapes
Not everything in the world is a rectangle, circle or triangle. In this tutorial, we give you practice at finding the perimeters and areas of these less-than-standard shapes!
-
Nets of polyhedra
We know...."nets of polyhedra" sounds like the title of a bad sci-fi movie about man-eating, muti-headed fish. A polyhedron ("polyhedra" is plural) is nothing more than a 3 dimensional shape with flat surfaces and straight edges (think: cube)
-
Finding surface area: nets of polyhedra
Now we shift our focus towards surface area (which is the sum of all the areas of all the shapes that cover the surface of the object). Let's apply it to the polyhedra net we learned about in the previous video. We'll walk you through it.
-
Find the volume of a triangular prism and cube
In this tutorial we'll practice finding solid geometry volume. Keep paper and pencil nearby in case you want to remember the formulas.
-
Cylinder volume and surface area
Finding the volume and surface area of a cylinder
-
How many people can a blimp carry
-
Volume of a cone
-
Volume of a sphere
Volume of a Sphere
Volume and surface area
Tired of perimeter and area and now want to measure 3-D space-take-upness. Well you've found the right tutorial. Enjoy!
-
Slice a rectangular pyramid
What happens when you slice vertically into a rectangular pyramid? What kind of geometric shape results?
-
Rotating 2D shapes in 3D