Khan Academy on a Stick
Exponents, radicals, and scientific notation
Understanding and solving exponents without algebra.
-
Exponentiation warmup
introduction to exponents and exponential growth
-
Introduction to exponents
Taking an exponent is basically the act of repeated multiplication. You know how to multiply, right? If so, understanding exponents is completely within your grasp!
-
Exponent example 1
-
Exponent example 2
-
Raising a number to the 0 and 1st power
The progression of powers from zero to any non-zero number follows a pattern and can be logically explained. After watching this, it will make sense why any non-zero number to the zero power equals one.
-
Powers of 1 and 0
Let's see what happens with bases to the zero power, plus we'll reinforce the patterns of applying exponents to postive and negative bases.
-
Powers of fractions
Just like whole numbers with exponents, fractions are repeatedly multiplied. If you know how to multiply factions, you're over half way there.
-
Powers of zero
We know that any non-zero number to the zero power equals one. We also know that zero to any non-zero exponent equals one. What happens when you have zero to the zero power?
The world of exponents
Addition was nice. Multiplication was cooler. In the mood for a new operation that grows numbers even faster? Ever felt like expressing repeated multiplication with less writing? Ever wanted to describe how most things in the universe grow and shrink? Well, exponents are your answer! This tutorial covers everything from basic exponents to negative and fractional ones. It assumes you remember your multiplication, negative numbers and fractions.
-
Understanding square roots
Understanding Square Roots
-
Approximating square roots
Approximating Square Roots
-
Simplifying square roots
-
Simplifying radicals
Using exponent rules to simplify radicals or square roots
-
Square roots and real numbers
-
Adding and simplifying radicals
More Simplifying Radical Expressions
The square root
A strong contender for coolest symbol in mathematics is the radical. What is it? How does it relate to exponents? How is the square root different than the cube root? How can I simplify, multiply and add these things? This tutorial assumes you know the basics of exponents and exponent properties and takes you through the radical world for radicals (and gives you some good practice along the way)!
-
Finding cube roots
Finding Cube Roots
-
Cube root of a non-perfect cube
-
Simplifying a cube root
Simplifying Radical Expressions1
The cube root
If you're familiar with the idea of a square root, we're about to take things one step (dimension?) further with the cube root. This generally refers to finding a number that ,when cubed, is equal to the number that you're trying to find the cube root of!
-
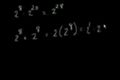Exponent rules part 1
Introduction to exponent rules
-
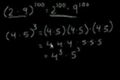Exponent rules part 2
2 more exponent rules with an introduction to composite problems
Exponent properties
Tired of hairy exponent expressions? Feel compelled to clean them up? Well, this tutorial might just give you the tools you need. If you know a bit about exponents, you'll learn a ton more in this tutorial as you learn about the rules for simplifying exponents.
-
Negative exponents
-
Negative exponent intuition
Intuition on why a^-b = 1/(a^b) (and why a^0 =1)
-
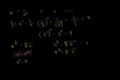Zero, negative, and fractional exponents
Zero, Negative, and Fractional Exponents
Negative and fractional exponents
It's normally a bad idea to hang around with negative people or do negative things, but we think it's OK to associate with negative exponents. And fractional exponents are even more fun. This idea will open up entirely new vistas to your mathematical life.
-
Introduction to scientific notation
Introduction to scientific notation. An in-depth discussion about why and how scientific notation is used.
-
Scientific notation
Scientific Notation
-
Scientific notation examples
More scientific notation examples
-
Scientific notation I
Scientific Notation I
-
Scientific notation example 2
Scientific Notation 2
Scientific notation
Scientists and engineers often have to deal with super huge (like 6,000,000,000,000,000,000,000) and super small numbers (like 0.0000000000532) . How can they do this without tiring their hands out? How can they look at a number and understand how large or small it is without counting the digits? The answer is to use scientific notation. If you come to this tutorial with a basic understanding of positive and negative exponents, it should leave you with a new appreciation for representing really huge and really small numbers!
-
Exponents and powers of zero patterns
Now that we understand how to interpret an exponent and how the patterns in zeros are related to the exponent, we can solve more complicated problems!
-
Orders of magnitude exercise example 1
-
Orders of magnitude exercise example 2
Orders of magnitude
When people want to think about the general size of things but not worry about the exact number, they tend to think in terms of "orders of magnitude". This allows us to analyze and make comparisons between numbers very quickly, which allows us to make decisions about them quickly as well.
-
Multiplying in scientific notation
u11_l1_t4_we_int Multiplying in Scientific Notation
-
Multiplying in scientific notation example
Multiplying in scientific notation example
-
Dividing in scientific notation example
Example showing how to divide two numbers expressed in scientific notation
-
Multiplying and dividing in scientific notation
-
Simplifying a complicated expression into scientific notation
-
Calculating red blood cells in the body using scientific notation
Computing with scientific notation
You already understand what scientific notation is. Now you'll actually use it to compute values and solve real-world problems.