Khan Academy on a Stick
Propriétés arithmétiques
Ce chapitre va vous permettre de vérifier si vous avez bien compris les bases de l'arithmétique. Vous allez faire le point sur les différentes façons de représenter des nombres entiers, la valeur de position, l'ordre des opérations, les arrondis et diverses autres propriétés.
La valeur de position
Il y a longtemps que vous savez compter. Vous passez sans y penser de "9" à "10" et de "99" à "100", mais que fait-on en réalité quand on ajoute un chiffre. Comment arrivons-nous à représenter tant et tant de nombres (en fait, autant de nombres que l'on veut) avec seulement 10 symboles (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) ? Dans ce chapitre, vous allez apprendre ce qu'on appelle la valeur de position. C'est indispensable pour comprendre ce que vous faites lorsque vous comptez. Cela peut changer pour toujours votre vision du monde !
Arrondir les nombres entiers
Si on cherche à construire un château avec des galets sur la plage, est-ce que ça change vraiment quelque chose si on a 19, 23 ou 25 galets ? Probablement pas. Tout ce qui compte, c'est d'avoir à peu près 20 galets pour que ça tienne. Dans ce module, nous allons voir comment arrondir les nombres entiers. C'est très utile quand on ne veut pas (ou on ne peut pas) être très précis.
Comprendre les représentations des nombres entiers
Nous allons essayer de comprendre les multiples façons de représenter un nombre entier, aussi bien avec des mots qu'avec des nombres. Nous allons même jouer avec la valeur de position pour vérifier que tout va bien !
Décomposer des nombres entiers
On casse la valeur de position d'un chiffre pour lui en retirer une partie que l'on donne à un autre chiffre. C'est une bonne façon de vérifier que vous avez compris ce qu'est la valeur de position. C'est aussi très utile quand on soustrait un nombre d'un autre (c'est ce que l'on appelle souvent "emprunter", même si vous ne "rembourserez" jamais cette valeur que vous prenez à un chiffre pour la donner à un autre).
Compter (en cours de traduction)
Combien doit-on faire de parts dans un gâteau ? De combien de poteaux a-t-on besoin pour la clôture ? Pour prendre ces décisions vitales il faut savoir bien compter.
Nombres rationnels et nombres irrationnels (en cours de traduction)
Vous n'imaginez probablement pas combien il y a de nombres qui ont le privilège de pouvoir s'écrire sous la forme d'un quotient de deux entiers. On les appelle les nombres rationnels. Mais il y a aussi une quantité d'autres nombres qui n'ont pas ce privilège. Comme vous l'aurez deviné, on les appelle les nombres irrationnels.
Ordre des opérations
Pour calculer "3 + 4 x 5", doit-on d'abord additionner 3 et 4, ou d'abord multiplier 4 par 5 ? Il n'y a pas de doute à avoir car le monde des mathématiques a défini des règles de priorité des opérations. Ceci est super important. Si vous hésitez, si ce n'est pas clair dans votre tête, vous ne pourrez pas faire grand chose de bon en mathématiques. Mais ne vous inquiétez pas, après ce chapitre vous aurez compris.
Distributivité
La distributivité de la multiplication sur l'addition est une idée que l'on retrouve sans arrêt en mathématiques. C'est l'idée que 5 x (3 + 4) = (5 x 3) + (5 x 4). Si cette définition est très claire pour vous, vous pouvez sauter ce chapitre. Si ce n'est pas trop clair, ou si vous ne savez pas pourquoi on peut écrire cette égalité, alors ce chapitre pourrait être une excellente occupation :)
-
 La loi commutative de l'addition
La loi commutative de l'addition
-
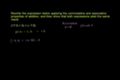 La propriété commutative de l'addition
La propriété commutative de l'addition
-
 La loi commutative de la multiplication
La loi commutative de la multiplication
-
 La loi associative de l'addition
La loi associative de l'addition
-
 La loi associative de la multiplication
La loi associative de la multiplication
-
 Utiliser les propriétés des opérations
Utiliser les propriétés des opérations
-
 Vocabulaire : les propriétés des opérations
Vocabulaire : les propriétés des opérations
-
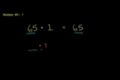 La propriété d'identité du chiffre 1 - Exemple 1
La propriété d'identité du chiffre 1 - Exemple 1
-
 La propriété d'identité du chiffre 1 - Exemple 2
La propriété d'identité du chiffre 1 - Exemple 2
-
 La propriété de neutralité du chiffre 0
La propriété de neutralité du chiffre 0
-
 L'opposé d'un nombre
L'opposé d'un nombre
-
 L'inverse d'un nombre
L'inverse d'un nombre
-
 Les propriétés des nombres - Exemple
Les propriétés des nombres - Exemple
Propriétés arithmétiques
2 + 3 = 3 + 2... ou 6 x 4 = 4 x 6... Additionner zéro à un nombre ne change pas le nombre. Multiplier un nombre par 1 ne le modifie pas non plus. Voici quelques exemples de propriétés utiles à connaître et qui portent parfois des noms compliqués. Découvrons les ensemble !

 Trouver la valeur de position d'un chiffre dans un nombre
Trouver la valeur de position d'un chiffre dans un nombre Ecrire avec des chiffres un nombre donné en toutes lettres
Ecrire avec des chiffres un nombre donné en toutes lettres Ecrire un nombre sous sa forme décomposée
Ecrire un nombre sous sa forme décomposée Arrondir des nombres entiers - Exemple 1
Arrondir des nombres entiers - Exemple 1 Arrondir des nombres entiers - Exemple 2
Arrondir des nombres entiers - Exemple 2 Arrondir les nombres entiers - Exemple 3
Arrondir les nombres entiers - Exemple 3 Comparer des nombres décomposés
Comparer des nombres décomposés Créer le plus grand nombre possible à partir d'une série de chiffres
Créer le plus grand nombre possible à partir d'une série de chiffres Décomposer des nombres entiers
Décomposer des nombres entiers Décomposer des nombres entiers - Exemple 1
Décomposer des nombres entiers - Exemple 1 Décomposer des nombres entiers - Exemple 2
Décomposer des nombres entiers - Exemple 2 Exercice de calcul
Exercice de calcul Introduction aux nombres rationnels et irrationnels
Introduction aux nombres rationnels et irrationnels Reconnaitre les nombres irrationnels
Reconnaitre les nombres irrationnels Introduction à l'ordre des opérations
Introduction à l'ordre des opérations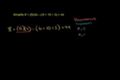 Ordre des opérations - Exemple 1
Ordre des opérations - Exemple 1 Ordre des opérations - Exemple 2
Ordre des opérations - Exemple 2 Ordre des opérations - Exemple 3
Ordre des opérations - Exemple 3 Introduction à la distributivité
Introduction à la distributivité  Distributivité de la multiplication
Distributivité de la multiplication Appliquer la distributivité dans des expressions algébriques
Appliquer la distributivité dans des expressions algébriques