Khan Academy on a Stick
Identités trigonométriques (en cours de traduction)
Symétrie et périodicité des fonctions trigonométriques
Dans ce module, nous poursuivons l'exploration du cercle trigonométrique afin de mieux apprécier le parti que l'on peut tirer des symétries. Nous allons aussi étudier la périodicité des fonctions (pourquoi elles se répètent après une certaine variation de l'angle).
L'identité trigonométrique de Pythagore
Dans ce module, nous nous intéressons aux relations entre les définitions du sinus, du cosinus et de la tangente (aussi bien dans le triangle rectangle qu'à partir du cercle trigonométrique) et le théorème de Pythagore pour obtenir et appliquer l'identité de Pythagore. Cette identité est à la base de beaucoup des autres identités trigonométriques, et ceci vous sera étonnamment utile toute votre vie !
Formule d'addition des angles
Nous allons maintenant voir que l'on peut exprimer sin(a+b) et cos(a+b) en fonction de sin a, sin b, cos a et cos b. Cela sera utile dans de nombreuses applications.
Démonstration des formules d'addition
Voyons si nous pouvons prouver les formules d'addition des angles pour le sinus et le cosinus !
Loi des cosinus et loi des sinus
Le premier outil que nous avions pour trouver la longueur d'un coté d'un triangle connaissant celles des deux autres était le théorème de Pythagore, mais celui-ci ne s'applique qu'à des triangles rectangles. Dans ce tutoriel, nous allons enrichir notre boite à outil de mesure de longueurs avec la loi des cosinus et la loi ds sinus. En utilisant ces outils, et en disposant de quelques informations sur la longueur des cotés et la mesure des angles, nous serons capables d'obtenir des résultats, même pour des triangles quelconques (c'est à dire pas forcément rectangles), ce qui pouvait vous paraître impossible à première vue !
Les identités trigonométriques
Si vous avez l'impression qu'il y a plus à faire avec les fonctions trigonométriques que ce qu'il semble à première vue, vous avez raison. Dans ce tutoriel, vous allez découvrir de belles, élégantes et hilarantes relations entre nos fonctions trigonométriques préférées (et peut être aussi quelques une qu'on apprécie pas particulièrement). Attention : Certaines de ces vidéos sont anciennes, filmées avec un équipement bon marché par Sal lui-même !

 Propriétés de symétrie des fonctions cos et sin
Propriétés de symétrie des fonctions cos et sin Propriétés de symétrie de la fonction tan
Propriétés de symétrie de la fonction tan Décalage d'un quart de tour
Décalage d'un quart de tour Quels sont les angles ayant une tangente de 0,5
Quels sont les angles ayant une tangente de 0,5 Application du théorème de Pythagore dans le triangle rectangle
Application du théorème de Pythagore dans le triangle rectangle Application du théorème de Pythagore dans le cercle trigonométrique
Application du théorème de Pythagore dans le cercle trigonométrique Application du théorème de Pythagore (exemple)
Application du théorème de Pythagore (exemple) Simplification d'une expression trigonométrique
Simplification d'une expression trigonométrique Sinus de l'addition de deux angles (exemple)
Sinus de l'addition de deux angles (exemple) Cosinus de l'addition de deux angles (exemple)
Cosinus de l'addition de deux angles (exemple) Cosinus de l'addition de deux angles (exemple 2)
Cosinus de l'addition de deux angles (exemple 2) Sinus d'un angle quelconque
Sinus d'un angle quelconque Cosinus de l'addition de deux angles (exemple 3)
Cosinus de l'addition de deux angles (exemple 3) Cosinus de l'addition de deux angles (exemple 4)
Cosinus de l'addition de deux angles (exemple 4) Démonstration de la formule d'addition pour la fonction sinus
Démonstration de la formule d'addition pour la fonction sinus Démonstration de la formule d'addition pour la fonction cosinus
Démonstration de la formule d'addition pour la fonction cosinus Loi des cosinus (ou théorème d'Al-Kachi)
Loi des cosinus (ou théorème d'Al-Kachi)  Loi des cosinus (exemple 1)
Loi des cosinus (exemple 1) Loi des cosinus (exemple 2)
Loi des cosinus (exemple 2) Loi des sinus
Loi des sinus Loi des sinus (exemple)
Loi des sinus (exemple) Démonstration de la loi des cosinus
Démonstration de la loi des cosinus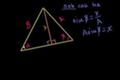 Démonstration de la loi des sinus
Démonstration de la loi des sinus Identités conséquences des deux formules d'addition
Identités conséquences des deux formules d'addition