Brüche : Khan Academy on a Stick

Khan Academy on a Stick

Arithmetik

Bruchrechnung - Einführung
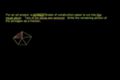Teile eines Bruchs bestimmen
Identifizierung Bruch Teile
Zähler und Nenner einer Bruchzahl
Lerne was der Zähler eines Bruchs ist. Lerne auch was der Nenner eines Bruchs ist.

Brüche verstehen

Wenn du Brüche nicht verstehst, wirst du nicht zu 1/3 ausgebildet sein. Ein Becher scheint halb leer statt halb voll zu sein. Du kannst dich glücklich schätzen, wenn du nicht von illegalen Immobiliengeschäften betrogen wirst oder viel zu viele Eier in deinen Kuchenteig rührst. Gut, dass dieses Tutorial hier ist. Du wirst sehen, dass Brüche uns eine ganz neue Sicht auf die Welt ermöglichen. Du wirst sehen, dass nicht immer alles ganze sein muss. Du wirst in der Lage sein zu schneiden, zu würfeln und es dann alles wieder zusammenzusetzen. (und wenn du jetzt bestellst, lagen wir einen Tortenheber ohne Aufpreis dazu.)

Gleichwertige Brüche - Textaufgabe Beispiel
Your teachers will tell you that being able to apply (or put to use) concepts helps you to learn them better. Here's a word problem in which you have to apply your knowledge of equivalent fractions.

Visualisierung gleichwertiger Brüche

Möchtest du lieber 2/3 oder 4/6 dieser Pizza? Es spielt keine Rolle, da beide Schreibweisen den gleichen Bruch darstellen. Dieses Tutorial wird uns helfen dies zu verstehen, indem wir visualisieren was gleichwertige Brüche repräsentieren.

Äquivalente Brüche
Einführung ins Konzept der äquivalenten Brüche
Equivalent fraction word problem example 4
Wie oft wurde dir schon gesagt, "Spare dein Geld!" Dachten wir. Was ist, wenn du einen Teil deines Taschengeldes sparen willst? Wie würdest du es angehen, um herauszubekommen wie viel du sparen musst?

Äquivalente Brüche und vereinfachte Form

Es gibt buchstäblich unendlich viele Möglichkeiten, jeden Bruch (oder auch jede Zahl) darzustellen. Glaubst du uns nicht? Nimm 1/3. 2/6, 3/9, 4/12... 10001/30003, das sind alles gleichwertige Brüche (und wir könnten da beliebig weitermachen)! If Wenn du weißt, was ein Bruch ist, dann ist dies ein großartiges Tutorial für das Erkennen von gleichwertigen Brüchen und das Vereinfachen dieser Brüche!

Vergleichen von Brüchen mit größer als und kleiner als Zeichen
Färbe visuelle Modelle von Brüche um Brüche zu vergleichen
Brüche mit gleichem Zähler und Nenner vergleichen

Brüche vergleichen

In diesem Tutorial trainieren wir unser Verständnis, welche Mengen durch Brüche eigentlich ausgedrückt werden und vergleichen diese Mengen.

Welchen Teil einer Stunde sollte Klavierspielen geübt werden? - Textaufgaben
Better get practicing, Pedro! You have exactly (a fraction) more of an hour to practice the piano.

Addieren und Subtrahieren von Brüchen

Du hast schon 2 Becher mit Zucker im Vorratsschrank. Das Rezept deiner Großmutter für diesen unverschämt süßen Kuchen verlangt 3 1/3 Becher mit Zucker. Wieviel Zucker müsstest du von deinem Roboter-Nachbarn ausleihen? Addition und Subtraktion von Brüchen ist der Schlüssel. Vielleicht ist es ratsam, das Tutorial für äquivalente Brüche anzusehen before du dieses Thema hier angehst.

Addieren und Subtrahieren von Brüchen
Wie man Brüche addiert und subtrahiert.

Brüche mit ungleichen Nennern addieren und subtrahieren

Wir hatten bereits einige gute Praxis darin, Brüche mit gleichen Nennern zu addieren. Wir machen wir das gleiche mit Brüchen mit ungleichen Nennern. Dies ist eine sehr große Sache. Nach diesem Tutorial wirst du so ziemlich alle zwei (oder drei oder vier oder...) Brüche addieren können!

Multiplizieren von Stammbrüchen und ganzen Zahlen
Lass dich nicht vom Multiplizieren ganzer Zahlen und Brüche unterkriegen. Wir können das. Diese Erklärung wird dir helfen, ein Profi zu werden.
Zwei Brüche multiplizieren - Beispiel
Lass uns zusammen üben, zwei Brüche zu multiplizieren. Wir werden auch lernen, die Antwort zu vereinfachen.

Brüche multiplizieren

Wie viel ist 2/3 von 2/3? Wenn 4/7 der Klasse Jungs sind, wie viele Jungs gibt es dann? Brüche multiplizieren zu können ist nicht nur super nützlich, sondern macht auch super viel Spaß.

Brüche Multiplizieren: Video-Marathon - Textaufgabe
Wir möchten einen Film-Marathon machen! Lass uns herausfinden, wie lang unser Marathon sein wird, wenn die Länge jedes Films durch eine gemischte Zahl dargestellt wird.
Brüche Multiplizieren: Die Liebe zur Milch - Textaufgabe
Wer mag schon Milch nicht gerne ? Unsere Familie tut es. Lasst uns herausfinden, wie viel Milch pro Monat verbraucht wird, wenn jede Person einen bestimmte Menge Milch verbraucht.
Brüche Multiplizieren : Der vertrackte Erdbeerkuchen - Textaufgabe
UUps! Jemand hat versucht diese Aufgabe zu lösen und einen Fehler gemacht. Schau ob du den Fehler erkennen kannst.
Brüche Multiplizieren: Das Bananenkuchen Rezept - Textaufgabe
We hope you learn to cook. Everyone should! At some point you'll need to make 1/2 a recipe which means using 1/2 of every ingredient in the recipe. Here's an example.
Textaufgabe Brüche Multiplizieren : Mit dem Rad zum Freund
You know how long it takes to bike to your friend's house, and you know how fast your can ride. So how far away does your friend live? The answer is one fraction multiplication problem away!

Multiplikation von Brüchen - Textaufgaben

Brüche multiplizieren zu können ist nützlich. Punkt. Das ist alles was wir dazu zu sagen haben. Glaub es uns oder nicht. Du wirst es schon noch lernen. In dieser Übung wirst du in realen Szenarien multiplizieren - was fast so viel Spaß macht wie komplett künstlich erstellte Szenarien.

Vergleich von unechten Brüchen und gemischten Zahlen
Beispiele zum Vergleich von unechten Brüchen und gemischten Zahlen
Gemischte Zahlen und unechte Brüche
Umwandeln von gemischten Zahlen in unechte Brüche und unechte Brüche in gemischte Zahlen
Gemischte Brüche in unechte Brüche umwandeln
Gemischte Brüche in unechte Brüche umwandeln
Einen unechten Bruch als gemischte Zahl schreiben
Lass uns unserem kopflastigen Freund, dem unechten Bruch, helfen, zu einer gemischten Zahl zu werden!
Dezimalzahlen und Brüche auf einer Zahlengeraden
Wir bringen es durcheinander, indem wir sowohl Dezimalzahlen als auch Brüche auf der gleichen Zahlengeraden unterbringen. Das ist eine sehr gute Übung, weil Sie sich mühelos zwischen den beiden bewegen müssen.

Gemischte Zahlen und unechte Brüche

Wir treffen oft auf Brüche, deren Zähler nicht kleiner als ihre Nenner sind (so wie 23/4 oder 3/2 oder auch 6/6). Diese schwerköpfigen Freunde heißen unechte Brüche. Da sie ein Ganzes oder mehr darstellen, können sie auch geschrieben werden als eine Kombination einer ganzen Zahl und eines echten Bruchs (ein Bruch, in dem der Zähler kleiner als der Nenner ist), was man auch 'gemischte Zahl' nennt. Das sind beides interessante Möglichkeiten, eine Zahl darzustellen, und beide (in diesem Tutorial) kennenzulernen wird im Leben supernützlich sein!

Gemischte Brüche addieren
Gemischte Brüche addieren

Multiplikation und Division von gemischten Brüchen

Du kennst die Grundlagen von gemischten Zahlen. Du bist jetzt bereit sie zu addieren und subtrahieren. Dieses Tutorial gibt dir ganz viele Beispiele und Übungen für diese wichtige Fähigkeit!

Dezimal zu vereinfachtem Bruch
Hier ein Beispiel, wie wir eine Dezimalzahl in einen vereinfachten Bruch umwandeln. Im Laufe der Zeit wird das wie eine zweite Natur für dich werden.
Bruchzahl zu Dezimalzahl
Das Umwandeln von Brüchen in Dezimalzahlen erfordert manchmal das Auffrischen unserer Kenntnisse von schriftlicher Division. Wir gehen das durch.
Bruch zu Dezimal mit Rundung
Manchmal wenn du einen Bruch in eine Dezimalzahl konvertierst musst du dividieren und runden.
Fraction to decimal example
Dies ist ein hervorragendes Beispiel wie man Brüche in Dezimalzahlen umwandelt. Verwende ein Blatt Papier um die Schritte aufzuschreiben und deutlich zu machen.
Brüche in Dezimalzahlen umwandeln
Wie ein Bruch als Dezimalzahl dargestellt werden kann
Umwandeln von Prozent in Dezimalzahl und Bruch
Du wirst bemerken, dass sich zwischen Prozent, Dezimalzahlen und Brüchen leicht hin und her zu bewegen äusserst hilfreich ist. Also lass es uns üben!
Dezimalzahlen in Brüche umrechnen - Beispiel 1
Lerne, wie man 0,15 in einen Bruch umwandelt.
Dezimalzahlen in Brüche umrechnen - Beispiel 2
Lerne, wie man 0,8 in einen Bruch umwandelt.
Dezimalzahlen in Brüche umrechnen - Beispiel 3
Lerne, wie man 0,36 als Bruch schreibt.
Umwandlung von Dezimalzahlen in Brüche 2 - Beispiel 1
Umwandlung von Dezimalzahlen in Brüche 2 - Beispiel 2
Ordnen von numerischen Ausdrücken
Ordnen von Zahlen in Form von Dezimalzahlen, Brüchen und Prozentsätzen
Umwandlung eines Bruches in eine periodische Dezimalzahl (Beispiel)
Lerne, wie man 19/27 als periodische Dezimalzahl aufschreibt. Was eine periodische Dezimalzahl ist? DAS ist eine gute Frage. Das Video erklärt's.

Dezimalzahlen und Brüche

Wenn du schon etwas über Dezimalzahlen und Brüche weißt, dann wird dieses Tutorial dir helfen, die Zusammenhänge zwischen den beiden zu verstehen. Mit einem Haufen Beispiele und Übungen wirst du dich bald in beiden Bereichen zu Hause fühlen. Viel Spaß!

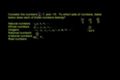Zahlenmengen
Zahlenmengen
Zahlenmengen 1
Zahlenmengen 1
Zahlenmengen 2
Zahlenmengen 2

Zahlenmengen

Die Welt der Zahlen kann aufgeteilt werden in mehrere "Sets ", von denen sich viele überlappen (ganze Zahlen, rationale Zahlen, irrationale Zahlen, etc.). Dieses Tutorial arbeitet mit Beispielen, in denen Sie mit der Terminologie vertraut gemacht werden und wie Sie sie unterscheiden können.