Khan Academy on a Stick
Étude et représentation graphique des fonctions affines
Utiliser le pouvoir de l'algèbre pour raisonner sur les points et les droites (ce qui habituellement relève de la géométrie). Nous apprendrons notamment à établir l'équation d'une droite.
Le plan repéré
Comment spécifier exactement où se trouve quelque chose dans le plan ? Qui était Descartes ? Dans ce module, nous allons d'abord définir ce qu'on appelle le plan repéré (ou plan cartésien). Puis nous verrons comment placer un point dans un repère, et comment déterminer si le couple de coordonnées d'un point est solution d'une équation à 2 inconnues. Ce module te sera utile aussi bien si tu commences tout juste à vouloir mieux comprendre les représentations graphiques, que si tu souhaites te réapproprier les bases.
-
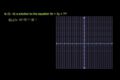 Déterminer une paire solution à une équation - Par substitution
Déterminer une paire solution à une équation - Par substitution
-
 Déterminer une paire solution à une équation - Méthode graphique
Déterminer une paire solution à une équation - Méthode graphique
-
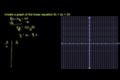 Dessiner les courbes représentatives de relations entre 2 variables
Dessiner les courbes représentatives de relations entre 2 variables
-
 Courbes représentatives de fonctions affines
Courbes représentatives de fonctions affines
-
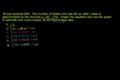 Problème : exemple d'utilisation d'une courbe représentative
Problème : exemple d'utilisation d'une courbe représentative
-
 Interpréter des courbes représentatives de fonctions affines
Interpréter des courbes représentatives de fonctions affines
-
 Explorer les relations linéaires
Explorer les relations linéaires
-
 Reconnaitre une fonction affine en utilisant le taux de variation
Reconnaitre une fonction affine en utilisant le taux de variation
-
 Dessiner les courbes représentatives de fonctions affines
Dessiner les courbes représentatives de fonctions affines
Représenter graphiquement les solutions d'une équation du 1er degré à 2 inconnues
Dans ce module, nous allons travailler sur des exemples qui montrent qu'une droite peut être considérée comme l'ensemble des points dont les coordonnées x et y satisfont à une équation du 1er degré à 2 inconnues. De même, une équation du 1er degré à 2 inconnues peut être considérée comme l'égalité qui lie les coordonnées x et y des points d'une droite.
-
 Dessiner des courbes à l'aide de l'abscisse et de l'ordonnée à l'origine 1
Dessiner des courbes à l'aide de l'abscisse et de l'ordonnée à l'origine 1
-
 Dessiner des courbes à l'aide de l'abscisse et de l'ordonnée à l'origine 2
Dessiner des courbes à l'aide de l'abscisse et de l'ordonnée à l'origine 2
-
 Abscisse à l'origine et ordonnée à l'origine 1
Abscisse à l'origine et ordonnée à l'origine 1
-
 Abscisse à l'origine et ordonnée à l'origine 2
Abscisse à l'origine et ordonnée à l'origine 2
-
 Déterminer l'abscisse à l'origine d'une droite
Déterminer l'abscisse à l'origine d'une droite
-
 Trouver l'ordonneÌe aÌ€ l'origine aÌ€ l'aide d'un tableau de valeurs et du taux de variation
Trouver l'ordonneÌe aÌ€ l'origine aÌ€ l'aide d'un tableau de valeurs et du taux de variation
-
 InterpreÌter l'abscisse et l'ordonneÌe aÌ€ l'origine et le taux de variation
InterpreÌter l'abscisse et l'ordonneÌe aÌ€ l'origine et le taux de variation
Points d'intersection avec les axes d'une droite représentative d'une fonction affine
Il y a plusieurs façons de tracer une droite et ce module traite de l'une des plus simples. Il suffit de deux points pour tracer une droite, donc on cherche la valeur de y lorsque x = 0 (l'ordonnée à l'origine) puis la valeur de x lorsque y = 0 (le point d'intersection avec l'axe des abscisses). Ensuite, on peut tracer la droite en reliant ces deux points.
Relations de proportionnalité
Dans ce module, nous allons étudier de plus près comment varie une grandeur en fonction d'une autre. Prêtes-y attention car tu vas vite te rendre compte que ce sont des idées que tu retrouveras durant toute ta vie !
Les taux dans les relations de proportionnalité
Dans les relations de proportionnalité, le rapport entre une variable et l'autre est constant. Dans le contexte des problèmes de taux, ce rapport constant peut aussi être vu comme un taux de variation. Ce module vous permet d'approfondir cette idée.
Coefficient directeur
Si vous avez déjà eu du mal à expliquer à quelqu'un à quel point un terrain était pentue, ce tutoriel est fait pour vous. En effet, nous y étudierons le concept de la pente d'une droite. Nous allons aussi découvrir en quoi cette pente est reliée à son équation et nous verrons comment on peut déterminer sa pente ou son intersection avec l'axe des ordonnées à partir de certaines données. Ce tutoriel s'adresse à ceux qui connaissent les bases des représentations graphiques d'équations et qui veulent aller un peu plus loin. Après ce tutoriel, vous serez préparés à étudier de façon plus poussée l'équation d'une droite.
Représentation graphique d'une équation de la forme y = ax + b
Ce qui fait la beauté des maths, c'est le nombre de façons différentes d'étudier la même relation. Dans ce module, nous allons nous servir de ce que nous savons sur le coefficient directeur pour tracer une droite d'équation y = ax + b.
Établir une équation de la forme y = ax + b
Le coefficient directeur et les points d'intersection avec les axes n'ont plus de secret pour toi. Nous allons utiliser ces savoir-faire pour déterminer l'équation d'une droite de la forme y = ax + b.
Équations de la forme y - b = m (x-a) et de la forme ax + by = c
Supposons que tu connaisses le coefficient directeur d'une droite et les coordonnées de l'un de ses points. Dans ce module, tu vas voir que tu peux utiliser ces informations pour déterminer rapidement l'équation de cette droite de la forme y - b = m (x - a) ! Tu apprendras aussi à passer de cette équation à l'équation de la forme y = ax + b et à l'équation de la forme ax + by = c.
-
 Coordonnées du milieu d'un segment
Coordonnées du milieu d'un segment
-
 Le théorème de Pythagore
Le théorème de Pythagore
-
 Calculer la distance entre deux points
Calculer la distance entre deux points
-
 Pentes de deux droites perpendiculaires
Pentes de deux droites perpendiculaires
-
 EÌquations de droites paralleÌ€les et perpendiculaires
EÌquations de droites paralleÌ€les et perpendiculaires
-
 EÌquations de droites paralleÌ€les
EÌquations de droites paralleÌ€les
-
 Droites parallèles
Droites parallèles
-
 Droites parallèles 2
Droites parallèles 2
-
 Droites parallèles 3
Droites parallèles 3
-
 Droites perpendiculaires
Droites perpendiculaires
-
 Droites perpendiculaires 2
Droites perpendiculaires 2
-
 Distance entre un point et une droite
Distance entre un point et une droite
Compléments de géométrie analytique
La droite représentative d'une fonction affine ou d'une fonction linéaire, son coefficient directeur et son ordonnée à l'origine sont des notions qui vous sont familières. Maintenant, on va aller plus loin en géométrie analytique en étudiant la distance entre deux points, les coordonnées du milieu d'un segment, les équations de deux droites parallèles et de deux droites perpendiculaires. Amusez-vous bien !
Résoudre graphiquement une inéquation du 1er degré
Dans ce chapitre, nous allons voir comment résoudre graphiquement une inéquation dans le plan repéré. Nous allons aussi apprendre à déterminer si le couple de coordonnées d'un point est, ou non, solution d'une inéquation.
Triangles semblables et coefficient directeur
Dans ce module, nous expliquons pourquoi le taux de variation m est le même entre deux points distincts quelconques d'une droite non verticale du plan repéré. Pour cela nous utiliserons des triangles semblables. Nous relierons cette idée à l'équation y = mx d'une droite passant par l'origine et à l'équation y = mx + b d'une droite coupant l'axe des ordonnées au point d'ordonnée b.
Taux de variation moyen
Même lorsqu'une la variation d'une fonction n'est pas linéaire, on peut calculer le taux de variation moyen sur un intervalle (mais on aura besoin de l'Analyse pour calculer le taux de variation pour une valeur particulière de la variable). Ce module va vous y entraîner.

 Descartes et les coordonnées cartésiennes
Descartes et les coordonnées cartésiennes Coordonnées cartésiennes
Coordonnées cartésiennes Placer des points dans le plan cartésien
Placer des points dans le plan cartésien  Les quadrants du plan
Les quadrants du plan  Comparer des relations de proportionnalité
Comparer des relations de proportionnalité DeÌterminer une eÌquation repreÌsentant une relation de proportionnaliteÌ
DeÌterminer une eÌquation repreÌsentant une relation de proportionnaliteÌ  ProbleÌ€me de taux de variation avec des fractions
Problème de taux de variation avec des fractions Problème de coût unitaire avec des fractions
Problème de coût unitaire avec des fractions Pente d'une droite
Pente d'une droite Pente d'une droite 2
Pente d'une droite 2 Pente d'une droite et taux de variation - Exercices
Pente d'une droite et taux de variation - Exercices  DeÌterminer graphiquement de la pente d'une droite
DeÌterminer graphiquement de la pente d'une droite  Pente d'une droite 3
Pente d'une droite 3 Exemple d'interpreÌtation de la pente d'une droite
Exemple d'interpreÌtation de la pente d'une droite  Exercices pour comprendre la notion de pente d'une droite
Exercices pour comprendre la notion de pente d'une droite  Tracer une droite aÌ€ partir de l'eÌquation d'une fonction affine
Tracer une droite aÌ€ partir de l'eÌquation d'une fonction affine  Transformer des eÌquations en eÌquations de fonctions affines
Transformer des eÌquations en eÌquations de fonctions affines  Introduction aux reÌgressions lineÌaires
Introduction aux reÌgressions lineÌaires  Passer d'une eÌquation aÌ€ sa repreÌsentation graphique
Passer d'une eÌquation aÌ€ sa repreÌsentation graphique DeÌterminer l'eÌquation d'une droite aÌ€ partir des coordonneÌes de deux points
DeÌterminer l'eÌquation d'une droite aÌ€ partir des coordonneÌes de deux points  Trouver l'ordonneÌe aÌ€ l'origine aÌ€ partir du coefficient directeur et d'un point
Trouver l'ordonneÌe aÌ€ l'origine aÌ€ partir du coefficient directeur et d'un point  EÌquation d'une droite sous la forme y - b = m(x - a)
EÌquation d'une droite sous la forme y - b = m(x - a)  EÌquation d'une droite sous la forme y - b = m(x - a) - Exercices
EÌquation d'une droite sous la forme y - b = m(x - a) - Exercices  Transformer l'eÌquation d'une droite sous la forme ax + by = c
Transformer l'eÌquation d'une droite sous la forme ax + by = c  Trois formes pour l'eÌquation d'une droite
Trois formes pour l'eÌquation d'une droite  Passer de la forme y - b = m(x - a) aÌ€ la forme y = mx + p
Passer de la forme y - b = m(x - a) aÌ€ la forme y = mx + p  RepreÌsentation graphique d'ineÌquations
RepreÌsentation graphique d'ineÌquations  RepreÌsentation graphique d'ineÌquation aÌ€ 1 inconnue
RepreÌsentation graphique d'ineÌquation aÌ€ 1 inconnue  Représentation graphique d'inéquations à 2 inconnues 1
Représentation graphique d'inéquations à 2 inconnues 1  Représentation graphique d'inéquations à 2 inconnues 2
Représentation graphique d'inéquations à 2 inconnues 2  Résolution graphique d'une inéquation
Résolution graphique d'une inéquation  Résolution d'inéquation
Résolution d'inéquation  Triangles semblables et coefficient directeur d'une droite
Triangles semblables et coefficient directeur d'une droite  Taux de variation moyen - Exercice 2
Taux de variation moyen - Exercice 2 Taux de variation moyen - Exercice 3
Taux de variation moyen - Exercice 3 Taux de variation moyen - Exercice 4
Taux de variation moyen - Exercice 4 Taux de variation et course à pied
Taux de variation et course à pied  Echelle d'un graphique
Echelle d'un graphique Taux de variation et freÌquence de rotation
Taux de variation et freÌquence de rotation