Khan Academy on a Stick
Développer ou factoriser une expression
Ce module va ajouter une tonne d'outils à ta boite à outils d'algèbre. Tu seras capable de multiplier n'importe quelles expressions et tu vas aussi apprendre à factoriser. Cela te permettra de résoudre toute une série de problèmes.
Multiplier et diviser deux monômes
"Monôme" semble un mot bien compliqué, pourtant il désigne des expressions simples comme "4x" ou "8xy" ou "17x^2z". Dans ce module, nous allons apprendre à les multiplier et à les diviser en utilisant des idées que vous connaissez (comme l'élévation à une puissance ou le plus grand diviseur commun).
-
 Développement d'un produit de binômes - problème
Développement d'un produit de binômes - problème
-
 "PEID" 4 lettres pour bien développer un produit de binômes
"PEID" 4 lettres pour bien développer un produit de binômes
-
 Développement d'un produit de binômes contenant des radicaux
Développement d'un produit de binômes contenant des radicaux
-
 Multiplying binomials and polynomials
Multiplying binomials and polynomials
-
 "PEID" 4 lettres pour bien développer un produit de binômes - exemple 2
"PEID" 4 lettres pour bien développer un produit de binômes - exemple 2
-
 Carré d'un binôme (identité remarquable)
Carré d'un binôme (identité remarquable)
-
 Identités remarquables 1
Identités remarquables 1
-
 Identité remarquable 2 (différence de 2 carrés)
Identité remarquable 2 (différence de 2 carrés)
-
 Carré d'un binôme 2
Carré d'un binôme 2
-
 Carré d'une différence (exemple)
Carré d'une différence (exemple)
-
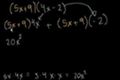 Produits classiques de binômes
Produits classiques de binômes
Multiplier deux binômes
Dans ce tutoriel tu apprendras que multiplier des choses comme (4x-7) et (-9x+5) ne requiert que la distributivité que tu connais depuis l'école primaire.
Factoriser une expression simple
Tu sais multiplier des expressions. Nous allons maintenant inverser le processus et voir des cas où il est possible d'écrire une expression sous la forme du produit d'autres expressions plus simples (comme nous l'avons déjà fait lorsque nous cherchions les diviseurs d'un nombre).
Factorisation d'expressions du second degré
La factorisation des polynômes du second degré est amusante, mais en plus elle est utile. Vous allez pouvoir résoudre toute une série d'équations. Et vous allez pouvoir aussi impressionner les gens dans les fêtes et faire une belle carrière. Super !
-
 Les identités remarquables
Les identités remarquables
-
 Factoriser une différence de 2 carrés - Exemple 1
Factoriser une différence de 2 carrés - Exemple 1
-
 Factoriser une différence de 2 carrés - Exemple 2
Factoriser une différence de 2 carrés - Exemple 2
-
 Factoriser pour arriver à une différence de 2 carrés
Factoriser pour arriver à une différence de 2 carrés
-
 Exemple : factoriser un trinôme comportant des carrés
Exemple : factoriser un trinôme comportant des carrés
-
 Factorisation d'un polynôme du 4ème degré
Factorisation d'un polynôme du 4ème degré
-
 Factoriser à l'aide des identités remarquables - exemple
Factoriser à l'aide des identités remarquables - exemple
Les identités remarquables
Vous allez rencontrer des expressions du second degré tout à fait factorisables et qui pourtant n'apparaissent pas toujours comme telles. Ce module va développer votre arsenal en vous apprenant à reconnaître une différence de deux carrés, le carré d'une somme ou le carré d'une différence.
-
 Factoriser en regroupant et factorisant complètement
Factoriser en regroupant et factorisant complètement
-
 Factoriser un trinôme en regroupant 1
Factoriser un trinôme en regroupant 1
-
 Factoriser un trinôme dont le premier coefficient est différent de 1
Factoriser un trinôme dont le premier coefficient est différent de 1
-
 Factoriser un trinôme en regroupant 2
Factoriser un trinôme en regroupant 2
-
 Factoriser un trinôme en regroupant 3
Factoriser un trinôme en regroupant 3
-
 Factorisation par la méthode des groupements (1)
Factorisation par la méthode des groupements (1)
-
 Factoriser un trinôme en regroupant 6
Factoriser un trinôme en regroupant 6
Regrouper pour factoriser
La plupart des gens ont du mal avec cette méthode. Ce n'est pas une raison pour que ce soit aussi votre cas. Dans ce module, vous allez voir que cette méthode permet aussi de factoriser un trinôme du second degré lorsque le coefficient du terme en x^2 est différent de 1.
Factoriser un polynôme du second degré de deux variables
Nous allons maintenant étendre l'application de nos outils de factorisation des trinômes du second degré, à la factorisation des expressions de 2 variables. Comme nous le verrons, il s'agit simplement d'une extension de ce que vous savez probablement déjà (ou au moins ce que vous saurez après être passé par ce module). En avant !
-
 Coefficients et degrés des termes d'un polynôme
Coefficients et degrés des termes d'un polynôme
-
 Un exercice intéressant sur les coefficients d'un polynôme
Un exercice intéressant sur les coefficients d'un polynôme
-
 Polynômes 1
Polynômes 1
-
 Polynômes 2
Polynômes 2
-
 Évaluer un polynôme en une valeur donnée
Évaluer un polynôme en une valeur donnée
-
 Simplifier un polynôme
Simplifier un polynôme
-
 Additionner deux polynômes
Additionner deux polynômes
-
 Addition de polynômes avec plusieurs variables (exemple)
Addition de polynômes avec plusieurs variables (exemple)
-
 Addition et soustraction de polynômes
Addition et soustraction de polynômes
-
 Somme et différence de polynômes 2
Somme et différence de polynômes 2
-
 Somme et différence de polynômes 3
Somme et différence de polynômes 3
-
 Somme et différence de polynômes 4
Somme et différence de polynômes 4
-
 Différence de polynômes
Différence de polynômes
-
 Soustraire deux polynômes de plusieurs variables
Soustraire deux polynômes de plusieurs variables
Qu'est-ce qu'un polynôme ?
"Polynôme" est un mot bien bien compliqué, mais il ne faut pas que vous vous attachiez aux apparences. "Poly" signifie plusieurs. Nous sommes donc juste en train de parler de "plusieurs nômes", et tout le monde sait ce qu'est un "nôme". En fait, non : la majorité d'entre nous en est incapable... Eh bien, un polynôme a plusieurs termes. En vous expliquant comment les "termes" des polynômes se simplifient, s'additionnent et se soustraient, se tutoriel va vous rendre très familier avec le monde des "plusieurs nômes." :)

 Produit de 2 monômes
Produit de 2 monômes Quotient de 2 monômes
Quotient de 2 monômes Produit et quotient de 2 monômes - 1
Produit et quotient de 2 monômes - 1 Produit et quotient de 2 monômes - 2
Produit et quotient de 2 monômes - 2 Produit et quotient de 2 monômes - 3
Produit et quotient de 2 monômes - 3 Plus grand facteur commun de 2 monômes
Plus grand facteur commun de 2 monômes Factorisation et propriété de distributivité
Factorisation et propriété de distributivité
 Factorisation d'expressions du premier degré
Factorisation d'expressions du premier degré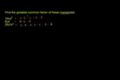 Factorisation et propriété de distributivité 2
Factorisation et propriété de distributivité 2 Factorisation et propriété de distributivité 3
Factorisation et propriété de distributivité 3 Factorisation à l'aide du plus grand facteur commun
Factorisation à l'aide du plus grand facteur commun Factorisation d'expressions du second degré
Factorisation d'expressions du second degré Factorisation d'expressions simples de degré 2 - exemple
Factorisation d'expressions simples de degré 2 - exemple Factorisation d'expressions de degré 2 - exemple
Factorisation d'expressions de degré 2 - exemple Factorisation d'un trinôme avec un facteur commun exemple
Factorisation d'un trinôme avec un facteur commun exemple Factoriser une forme quadratique avec 2 variables
Factoriser une forme quadratique avec 2 variables Factoriser une forme quadratique avec 2 variables - Exemple
Factoriser une forme quadratique avec 2 variables - Exemple Produit d'un polynôme par un monôme
Produit d'un polynôme par un monôme Produit de polynômes (1)
Produit de polynômes (1)  Produit de polynômes (2)
Produit de polynômes (2)  Encore des produits de polynômes
Encore des produits de polynômes