di Paolo G. Calisse
Ci si può chiedere quale sia la probabilità che un evento del tipo
di quello segnalato da Paolo
in un suo precedente articolo
- un personaggio del calibro di George Lucas che appare
casualmente sullo sfondo di un video di YouTube - accada
realmente. Ho tentato di fare una stima usando un approccio molto
semplice e lineare. Potete farlo anche voi copiando l'algoritmo
ottenuto più in basso in un foglio di calcolo e inserendo i dati
di ingresso che ritenete più ragionevoli, per verificare se la
coincidenza sia spettacolare o rientri tutto sommato nella
normalità delle cose. La mia stima si basa ovviamente su un numero
di assunzioni che discuto nel seguito.
Alla ricerca dell'algoritmo
Chiamiamo per prima cosa Nvid il numero di video ripresi
per strada e disponibili su Youtube. Supponiamo per cominciare che
Nvid = 1.000. Assumiamo inoltre che ci siano
Nvip personaggi noti del calibro di Lucas che saremmo
sorpresi di incontrare in uno di questi video e che
Nvip = 1.000. Troppi? Pochi? Ne discuteremo più oltre. Per
semplicità, possiamo ritenere che tali VIP siano distribuiti
uniformemente su tutto il territorio USA, dove
Ntot = 328 milioni di persone, e che seguano le stesse
abitudini di noi comuni mortali nel circolare per strada: orari,
distribuzione, etc. In mancanza di informazioni più precise non
possiamo fare altro che accettare questa assunzione, su cui
comunque torneremo in seguito.
Ora, se ci sono Nvip volti noti distribuiti uniformemente
tra Ntot persone, la probabilità che qualcuno sia un VIP
sarà Nvip/Ntot e quindi la probabilità - molto alta - che
non lo sia:
1-Nvip/Ntot
Infatti la somma delle probabilità di non conoscere o di conoscere
almeno una persona deve essere per forza di cose pari ad uno.
Immaginiamo adesso che in ogni video si vedano in genere
Np persone riconoscibili passare sullo sfondo. Assumiamo
per adesso che Np = 10. Si tratta probabilmente di una
grossolana sottostima, considerata la durata tipica di molti di
questi video.
Ora, se i video sono Nvid, il numero totale di
persone riconoscibili che passano sullo sfondo del numero totale
di video disponibili sarà Nvid*Np. A questo punto non
dovrebbe essere difficile convincersi che la probabilità che
nessuno di costoro sia un volto noto sarà:
(1-Nvip/Ntot)*(1-Nvip/Ntot)*...*(1-Nvip/Ntot)
dove il prodotto viene ripetuto Nvid*Np volte ovvero
(1-Nvip/Ntot)^(Nvid*Np)
che è il prodotto della probabilità che ciascuna delle persone
visibili in tutti i video disponibili sia un comune mortale. A
questo punto per sapere qual è la probabilità che
almeno uno di costoro sia un volto noto basterà
semplicemente calcolare la differenza tra uno e la probabilità
precedente. Si ottiene quindi:
P = 1-(1-Nvip/Ntot)^(Nvid*Np)
che ci consente di stimare la probabilità di scoprire un volto
molto noto all'interno di uno di quei video.
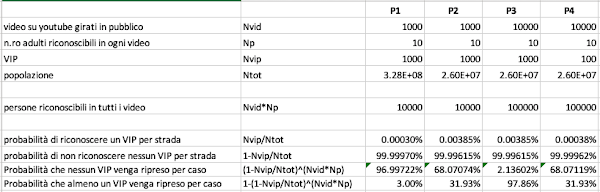
Proviamo adesso a inserire in questa semplice formula le stime
precedenti:
-
Nvip = 1.000 = personaggi noti quanto Lucas presenti
sul territorio USA in ogni momento. Questo numero includerà
politici, sportivi famosi, personaggi dello spettacolo, etc.
- Ntot = 328.000.000 = popolazione USA
-
Nvid = 1.000 = numero totale di video abbastanza
popolari disponibili su YouTube e registrati in pubblico
-
Np = 10 = numero medio di persone che passano sullo
sfondo di ciascuno di quei video.
Il risultato che si ottiene inserendo questi dati nell'algoritmo
che ho ottenuto sarà un misero P1 = 3%. Sembrerebbe quindi che in effetti la probabilità di vedere
almeno un volto noto passare per caso sullo sfondo di
uno dei video presenti su YouTube sia piuttosto bassa,
anche ammettendo che vengano riconosciuti tutti.
Ma a pensarci bene VIP e riprese non sono distribuiti a caso su
tutto il territorio USA ma accentrati in luoghi specifici.
Difficile infatti trovare un video del genere di quello mostrato
girato nelle sconfinate praterie USA o in un microscopico
villaggio del Midwest o dell'Alaska. Molto più probabile trovarne
di ambientati per le strade del centro di Los Angeles o New
York.
Assumiamo allora
che gli stessi video vengano girati tutti nelle
10 più popolose aree urbane USA, ovvero Los Angeles, New York, Chicago, etc. fino alla già meno
nota San José. In questo caso
Ntot = 26 milioni di abitanti. Probabilmente stiamo ancora
sovrastimando il modo con cui si comportano questi VIP, certamente
più abituati a frequentare grandi alberghi o quartieri altolocati
che malfamate e insicure periferie cittadine. Comunque sia,
assumiamo che in queste 10 città vi siano in ogni dato
momento almeno 1.000 VIP. In effetti solo Los Angeles e New York
ospitano probabilmente centinaia di attori che vivono e lavorano
in un'area ristrettissima popolata da pochi milioni di abitanti.
Applicando lo stesso algoritmo con i nuovi dati:
Nvid = 1.000
Np = 10
Nvip = 1.000
Ntot =26.000.000
il risultato cresce ad un sorprendente P2 = 32%.
In alternativa, considerato che YouTube ospita circa
2 miliardi e mezzo di video, è certamente possibile che vi siano però almeno
10.000 video girati in pubblico e che abbiano un numero di
visitatori tale da permettere a qualcuno di notare una persona
importante sullo sfondo. Anche considerato che il "pyroprocessing"
non è esattamente un argomento alla moda e nonostante questo il video considerato nell'articolo
cattura l'attenzione di oltre 4 milioni di spettatori!
Se così fosse la probabilità di avere almeno un video con un VIP
sullo sfondo crescerebbe fino alla quasi assoluta certezza:
P3 = 98%.
Sono possibili altre variazioni sul tema. Per esempio si può
assumere che il numero di VIP resti uguale a prima ma che il numero di video sia
superiore di altrettanto (Nvid = 10.000).
Nvid = 10.000
Np = 10
Nvip = 1000
Ntot = 26.000.000
In tal caso il risultato salirebbe alla quasi certezza
P3 = 98%.
Si può anche essere meno "ottimisti" e considerare il caso di
10.000 video ma 100 VIP che si aggirano per le 10 città più
importanti. In questo caso
Nvid = 10.000
Np = 10
Nvip = 100
Ntot =26.000.000
la probabilità torna ad essere straordinariamente simile al caso
P2: P4 = 32%. La similarità tra i due casi è abbastanza
sorprendente in effetti e dovuta anche all'arrotondamento.
Noto infine che il risultato dipende unicamente da
Np*Nvid e Nvip/Ntot, non dai 4 dati in ingresso.
Quindi, fino a quando questi due fattori restano
identici, il risultato sarà sempre lo stesso.
Nella figura che segue ho riportato tutti i casi che ho
considerato. Copiando l'algoritmo il lettore può divertirsi a
trarre le proprie stime.
Conclusioni
Se questa stima non è in grado di valutare con precisione
sufficiente quale sia la probabilità di individuare un qualche VIP
per caso su YouTube, mostra tuttavia che con una scelta comunque
ragionevole dei parametri in gioco la probabilità di trovarne
prima o poi uno non è così bassa come si potrebbe ritenere a prima
vista.
Si potrebbe anche obiettare
che in realtà la probabilità che cerchiamo sia quella di trovare
George Lucas, e non "un VIP qualsiasi" sullo sfondo di un video.
Ma attenzione, bisogna stare attenti a definire correttamente la
peculiarità di quel video: l'aspetto curioso non è che
Lucas sia stato ripreso fortuitamente in un video che parla di
pyroprocessing, ma che un personaggio molto noto sia stato ripreso
in un video abbastanza popolare presente su YouTube. Se
infatti si fosse trattato di Ridley Scott, di James Cameron* o di
uno fra le migliaia di personaggi del mondo dello spettacolo,
della cultura (immaginate di scorgere Stephen King, sapreste riconoscerlo?) o della politica, non sareste rimasti ugualmente
stupiti?
E' anche interessante che lo stesso algoritmo può essere
facilmente applicato, con qualche piccola variazione, a molte
altre situazioni. Per esempio alla probabilità di incontrare un
vecchio compagno di scuola per caso nella nostra città. Lascio al
lettore questo facile esercizio.
* Come ho raccontato tempo addietro in un commento su questo
stesso blog, mi è capitato per caso di conversare per diverse
ore proprio con James Cameron, ma senza avere idea di chi
fosse. In quell´occasione gli ripetei più volte, dopo che mi
aveva detto di "lavorare nel cinema" e di "avere lavorato in
film come Terminator" (almeno così mi era sembrato di capire
con il mio pessimo inglese dei tempi) che... a me purtroppo i
film di quel genere non sono mai piaciuti. Ma eravamo entrambi
su un C-130 semivuoto diretto dalla base USA di McMurdo a
quella di South Pole, non proprio una situazione comune. Il
che rende questa analisi probabilistica del tutto
inapplicabile.